Predicting Growth of a Social Network

Why Social Networks Are So Hard for Marketers

The conundrum of launching a network is how do you get early users (i.e. customers) to join when you have so few on the network? In short, every purchaser of technology in the 20th century (and for most of time) has had to ask themselves, “Is this thing really worth the hassle of signing up?”

Imagine how hard it would be to sell the first telephones when hardly anyone else can use it. It takes a special demographic to be an initial buyer of such a disruptive technology. But as more and more people buy a telephone (and thus join the network) it becomes increasingly important for non-users to own one as well. After all, the value in joining a network is the experience of the interactions with other users that occur by being on one network.

How to Build a Network

Back to marketing the first telephones: As a marketer, you’d maybe position the product on user cases that they need a telephone to connect with loved ones. Or for emergencies. Or to do business. These special cases start to represent strong value propositions for a new user to adopt the technology.

Note: This is very important. If the network can establish brand dominance, it will over time literally force users to join if they want to interact with other users. The power of the network becomes too strong to resist adoption and literally pulls users in if they want to communicate with their social circle. (Facebook has executed brilliantly on this fact.)

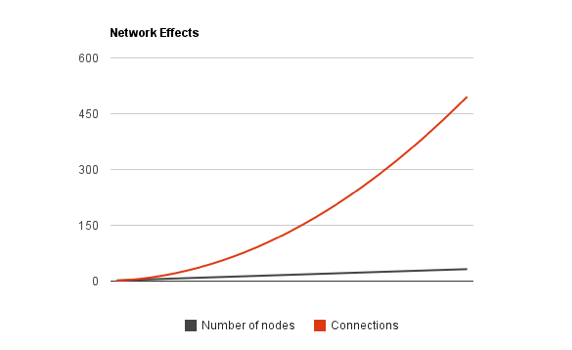
Therein lies the strong impetus for a new user to join the network and is essentially what Metcalfe’s Law is all about – that the number of unique connections in a network due to the number of nodes can be roughly expressed mathematically as n(n-1)/2.

Which means:

• Two telephones can only make one connection: 2((2-1)/2) = 1. So the “value” is roughly one. Not much right?

• But five telephones can make ten connections. 5((5-1)/2) = 5*2 = 10

• And Twelve can make 66 connections. 12((12-1)/2) = 12(6.5) = 66

If we were to plot these numbers, we would start to see some interesting growth…

Notice how the number of nodes being added (telephones in this example) grows at a fairly predictable clip over time? A mathematician would call it linear growth.

But the connections representing value in red, while growing at a fairly steady rate at first, all the sudden increase very quickly over time despite the fact that the number of telephones being added is nowhere near as rapid.

Key Concept: So with just a few more nodes added, the network suddenly becomes way, way more valuable due to all the connections created exponentially thanks to Metcalfe’s Law.

This is what mathematicians call exponential growth and is at the heart of how things like Facebook can go from 0 users to 800 million in only seven years. (It’s also the classic “hockey stick” chart that every starry-eyed web entrepreneur puts into their business plans to pitch to venture capitalists.)

And this growth is incredibly difficult to achieve.

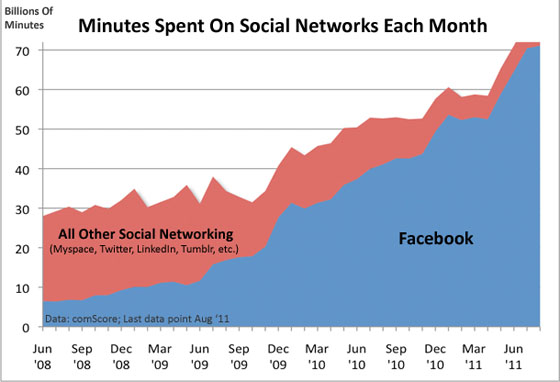
Let’s compare Facebook’s growth against the above chart example for telephones – do you see the obvious overlap of Metcalfe’s Law visually?

Here in this example, we can use minutes spent on a social network as a proxy for measuring the value of that network. We see that Facebook bumps along at a fairly linear rate from June to September in 2008. Than it starts to climb as more people join the network. In June 2009, it takes off and does not slow down in its quest to dominate our time against all other social networks.

This is Metcalfe’s Law in action.

Source: Comscore

While room for debate remains on whether Metcalfe or Reed’s Law is correct when applied to the web, the big idea to keep in mind is that networks can scale to large numbers very quickly – commonly referred to as exponential growth. The near instantaneous nature of the Internet is what helps make this exponential growth possible. We’ll come back to this later when we discuss viral marketing and why things spread across a network very quickly but now you understand how.

It is worth noting that Metcalfe’s Law is not an absolute perfect law. The “value” of the network is highly dependent on the user’s pain points but nonetheless it represents a good rule of thumb to consider when considering ramping up an online community and staying motivated when the growth does not immediately happen. If we look at the chart, we see quite a bit of time where the value and the connections barely climb at the same rate. This linear growth was true even for Facebook up until roughly June 2009.

Perhaps there is no better ironic example of network theory than that of grandparents who grew up with a young technology called the telephone and are today joining Facebook to communicate with their grand kids.